Consistent Hashing

Terminology

• Node: a server that provides functionality to other services.
• Hash function: maps data of arbitrary size to fixed-size values.
• Data partitioning: distributes data across multiple nodes to improve performance and scalability.
• Data replication: stores multiple copies of the same data on different nodes to improve availability and durability.
• Hotspot: a performance‑degraded node due to a large share of data and high request volume.

---

Requirements

• Minimise hotspots.
• Handle Internet‑scale, dynamic load.
• Minimise data movement when nodes join/leave.

---

Why Consistent Hashing?

Popular sites can spike in traffic quickly. Caches reduce load/latency, but the cache tier must scale elastically. A fixed pool of cache servers can’t keep up with dynamic demand. Consistent hashing lets us scale the cache tier up/down while moving only a small fraction of keys.

Replication vs. Sharding (Partitioning)

Replication

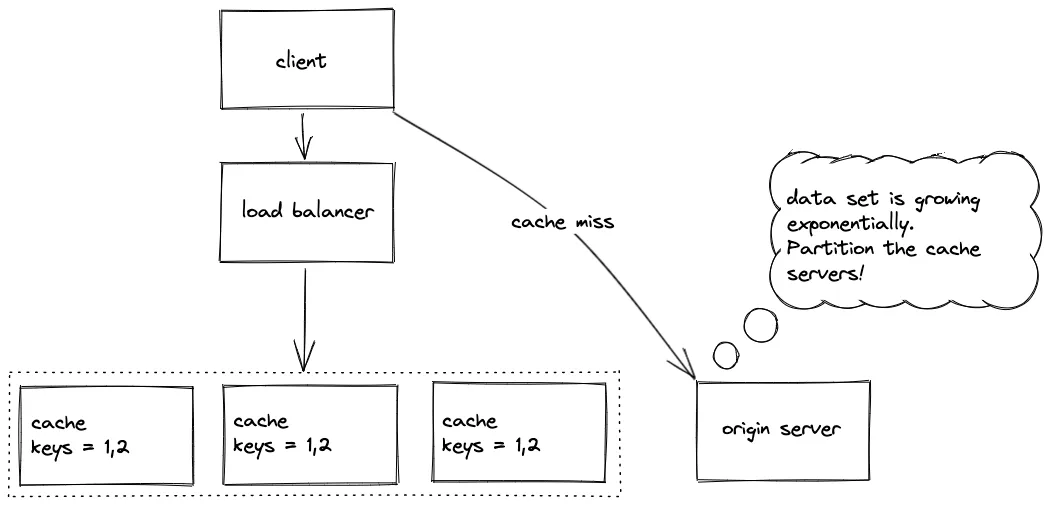
Replication improves availability and read throughput, but does not on its own solve dynamic load because only a limited subset of data can be cached and keeping replicas strongly consistent is costly.

Problems

• Limited cacheable dataset.
• Maintaining consistency between replicas is expensive.

Sharding (Partitioning)

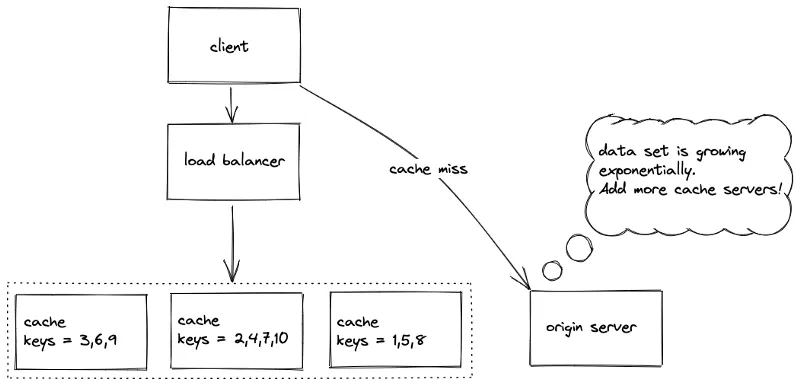
Sharding is how we scale horizontally. Data is split across nodes; replication is orthogonal (you can shard and replicate). Multiple shards can live on one node to improve fault tolerance and throughput.

Reasons to shard

• Cache servers are memory‑bound.
• Higher parallelism → higher throughput.

---

Partitioning Approaches (Quick Compare)

• Random Assignment

  • ✅ Simple.
  • ❌ Uncontrolled distribution → hotspots likely.

• Single Global Cache

  • ✅ Easy to manage for tiny datasets.
  • ❌ Scalability bottleneck & single point of failure.

• Key Range Partitioning

  • ✅ Efficient range queries.
  • ❌ Skewed ranges create hotspots; hard to rebalance as data evolves.

• Static Hash Partitioning (mod N)

  • ✅ Deterministic, balances typical loads.
  • ❌ When N changes (nodes join/leave), almost all keys move (rehash to new mod), causing churn.

Takeaway: Hashing is great for balance; consistent hashing fixes the “mod N changes” churn problem.

---

Consistent Hashing (What & How)

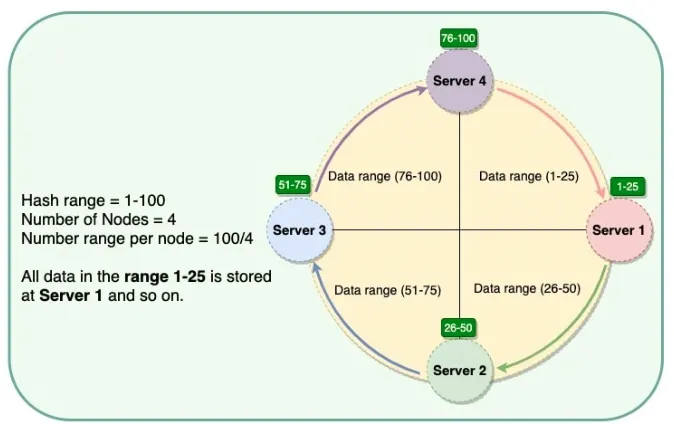
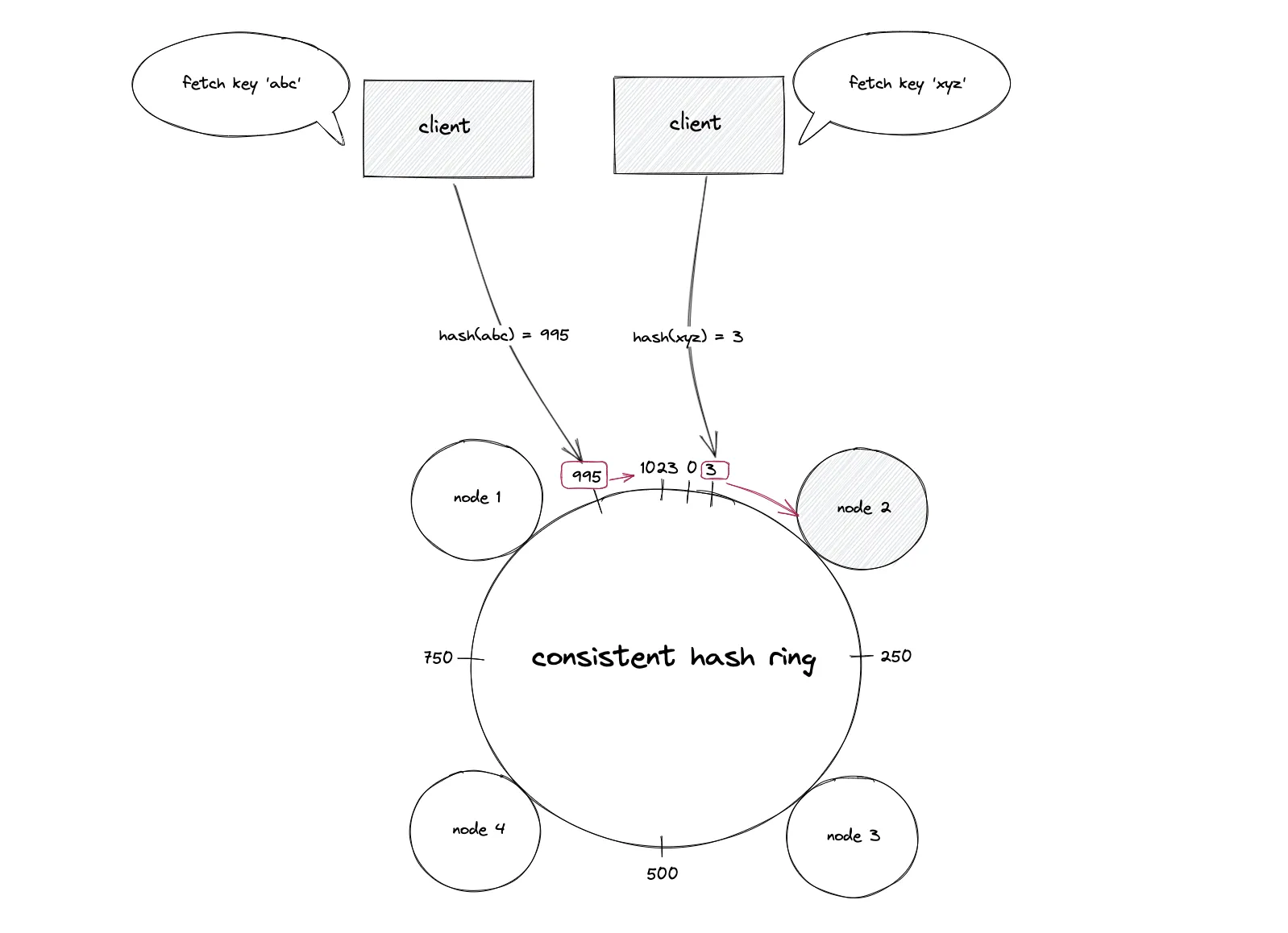
Idea: Place both nodes and keys on a circular hash ring (0…2^m−1). A key belongs to the first node clockwise from its hash position. When nodes join/leave, only keys on the affected arcs move.

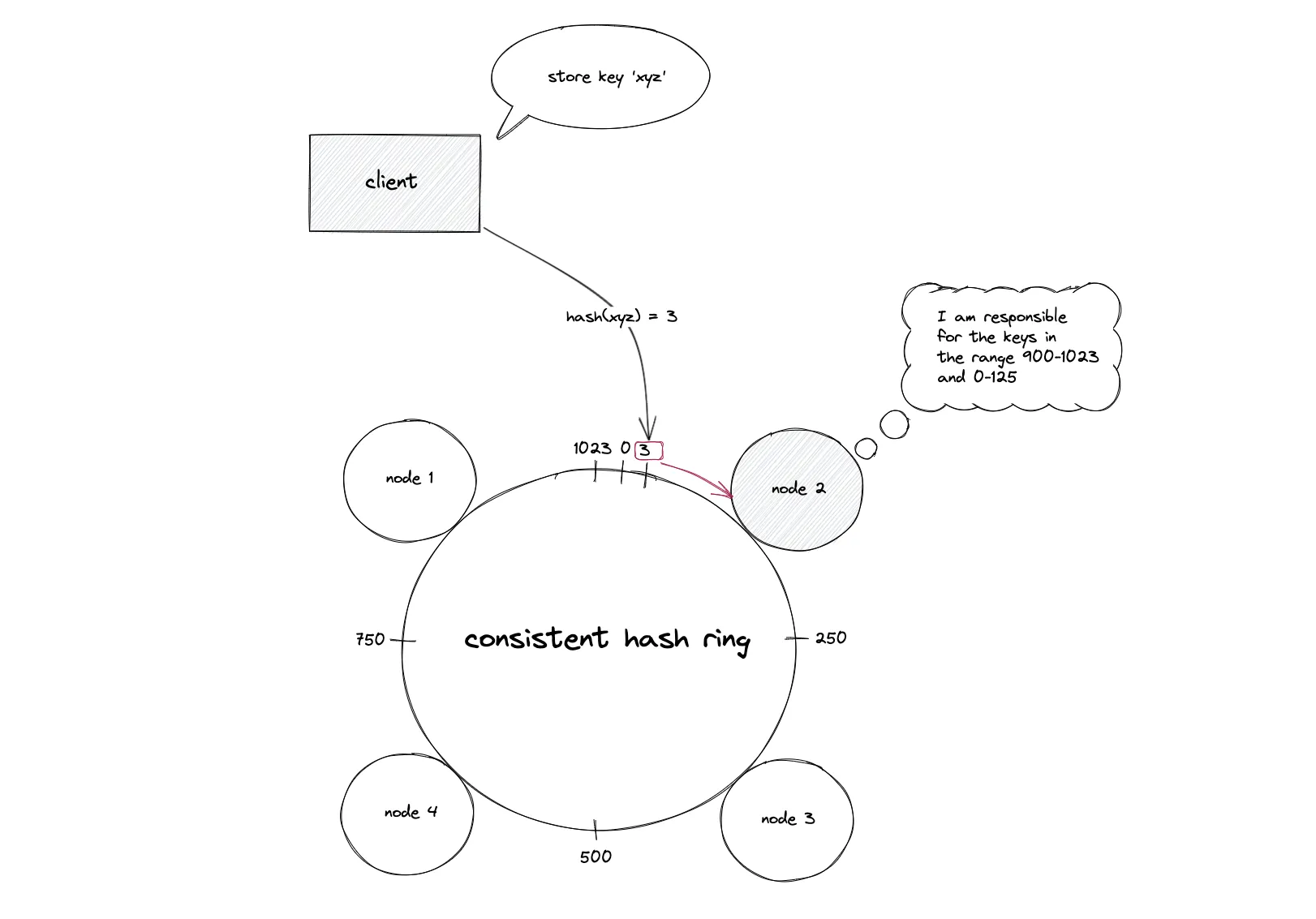
Lookup: Hash the key → walk clockwise to the successor node.

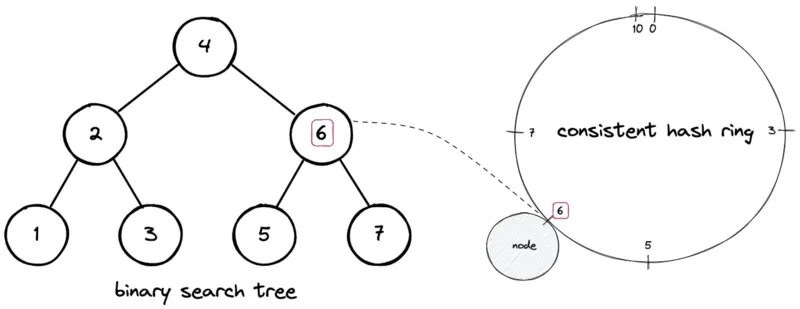
Data structure: Keep node positions in an ordered map (e.g., self‑balancing BST / TreeMap). Search/insert/delete are O(log N).

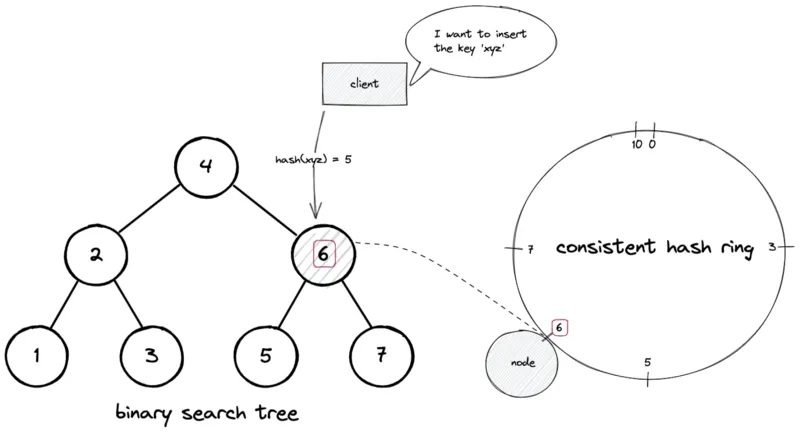
Example: key xyz hashes to 5 → successor node is at position 6 → store on node at 6.

Operations

1. Insertion

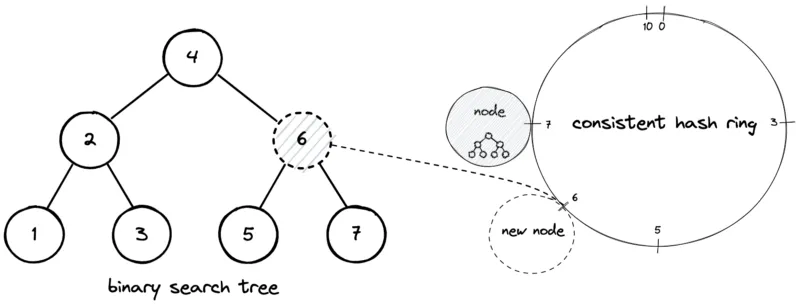
Steps: hash(key) → successor(node) in the ring → store.

2. Deletion

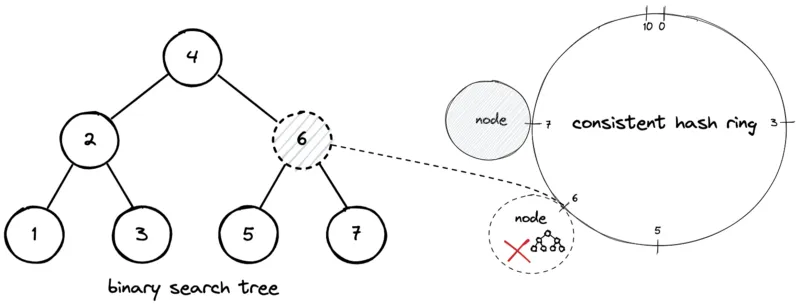
When a node leaves, only the keys it owned move to the next clockwise node.

Why it meets the requirements

• Scalable: distributes keys over many nodes.
• Low movement: only nearby keys remap on membership change.
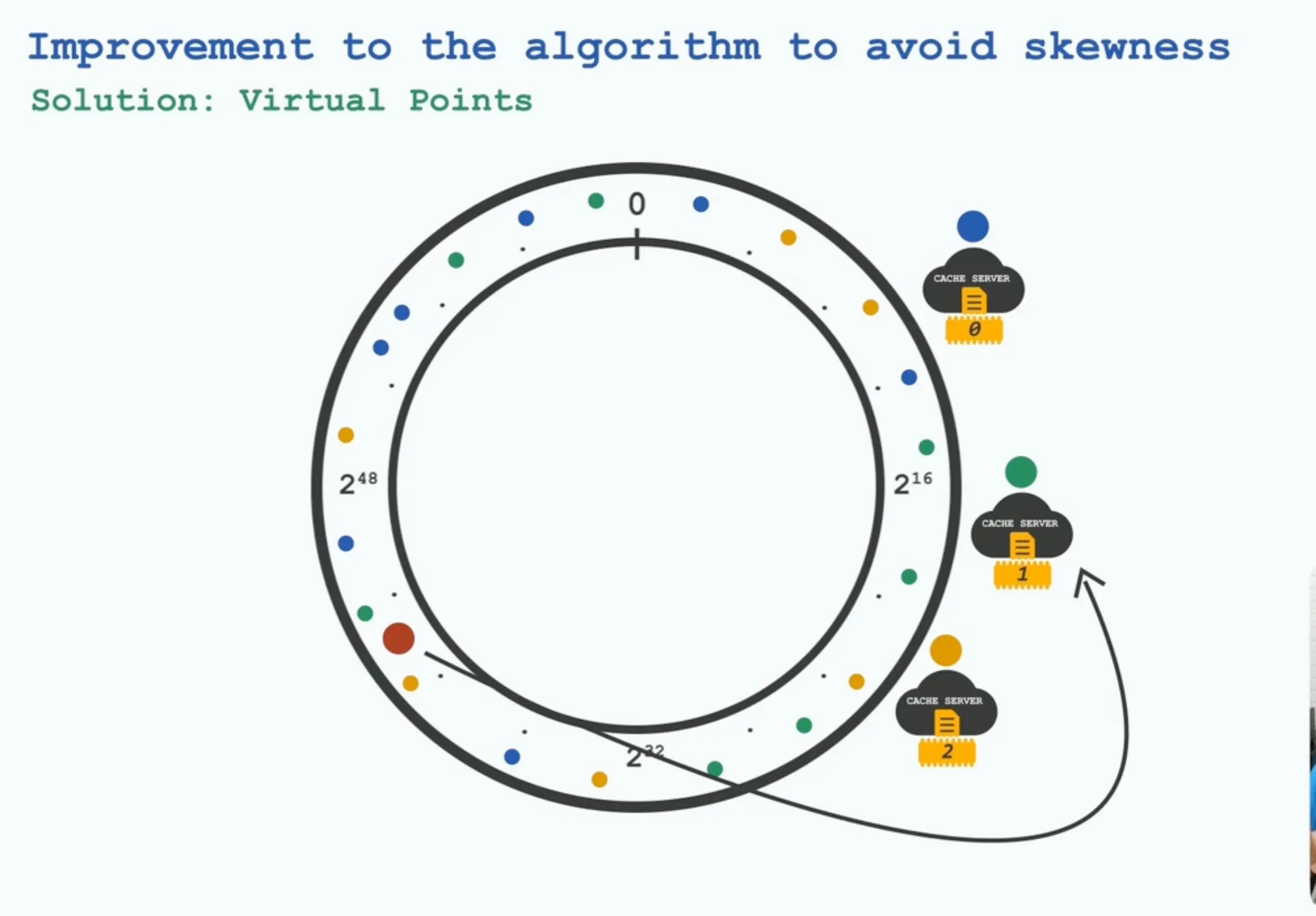
• Hotspot mitigation: use virtual nodes and weights; add capacity by adding nodes or increasing a node’s weight (more virtual nodes) without reshuffling everything.

---

Practical Tips

• Virtual Nodes (VNodes): insert each physical node multiple times on the ring to smooth distribution.
• Weighted nodes: more vnodes for stronger machines.
• Replication on the ring: place each key on the next R distinct nodes clockwise to improve availability.
• Hash choice: a uniform, fast hash (Murmur3, xxHash). For simplicity in demos, String.hashCode() is fine; in prod, prefer a better hash.
• Failure handling: on node failure, keys fall through to the next successor automatically.
• Monitoring: watch key/traffic distribution; consider adaptive weights if skew emerges.

---

Complexity

• Add/Remove Node: O(V log N) where V = virtual nodes for that machine.
• Lookup (getNode): O(log N).
• Movement on change: ~O(K/N) keys move (K = total keys, N = nodes).

---

Java Code (Simpler & Clearer)

A small, generic implementation using TreeMap and optional replication. It keeps the original spirit, adds clear comments, and makes VIRTUAL_NODES configurable. The hash is kept simple for readability; swap it with a stronger hash if needed.

import java.util.*;

class ConsistentHashing {
    private final TreeMap<Integer, String> ring = new TreeMap<>();
    private final int VIRTUAL_NODES = 3;  // Virtual nodes to balance the distribution
    private final int HASH_SPACE = Integer.MAX_VALUE;  // 32-bit hash space

    private int hash(String key) {
        return key.hashCode() & HASH_SPACE;  // Simple hash function
    }

    public void addNode(String node) {
        for (int i = 0; i < VIRTUAL_NODES; i++) {
            int hash = hash(node + i);
            ring.put(hash, node);
            System.out.println("Added node " + node + " with hash " + hash);
        }
    }

    public void removeNode(String node) {
        for (int i = 0; i < VIRTUAL_NODES; i++) {
            int hash = hash(node + i);
            ring.remove(hash);
            System.out.println("Removed node " + node + " with hash " + hash);
        }
    }

    public String getNode(String key) {
        if (ring.isEmpty()) return null;
        int keyHash = hash(key);
        // Find the next node in the hash ring (circular behavior)
        Map.Entry<Integer, String> entry = ring.ceilingEntry(keyHash);
        if (entry == null) {
            return ring.firstEntry().getValue();  // Wrap around to the first node
        }
        return entry.getValue();
    }

    public void printRing() {
        System.out.println("Hash Ring: " + ring);
    }

    public static void main(String[] args) {
        ConsistentHashing ch = new ConsistentHashing();

        // Adding nodes
        ch.addNode("Node1");
        ch.addNode("Node2");
        ch.addNode("Node3");

        ch.printRing();

        // Mapping some keys
        System.out.println("Key 'Apple' is assigned to " + ch.getNode("Apple"));
        System.out.println("Key 'Banana' is assigned to " + ch.getNode("Banana"));

        // Removing a node
        ch.removeNode("Node2");

        ch.printRing();

        // Checking mapping after removal
        System.out.println("Key 'Apple' is now assigned to " + ch.getNode("Apple"));
        System.out.println("Key 'Banana' is now assigned to " + ch.getNode("Banana"));
    }
}